글수 792
(작년의 내용을 보완해서 올립니다.)
Matlab으로 시뮬레이션하였습니다. 파일첨부가 안돼서 m-file을 올리지 못하여 그냥 긁어 붙입니다. 실행해보는 방법은 다음과 같습니다.
1. MATLAB에 File->New->M-file여시고 아래 내용을 긁어다 붙입니다.
2. 저장하실 때 dicful.m으로 저장합니다. (아마 default로 되어있을 겁니다.)
3. command 창에서 dicful(샘플수, 시뮬레이션 반복 수)를 입력하고 엔터.
ex) 1000개의 샘플을 가지고 10000번 시뮬레이션 돌리고 싶으면, dicful(1000,10000) 입력
function f=dicful(smpl, repl)
Y=zeros(smpl+1,1);
Y_1=zeros(smpl+1,1);
rhohat=zeros(repl,1);
tau=zeros(repl,1);
for j=1:repl
randn('state',j)
e=randn(smpl,1);
for i=1:smpl
Y(i+1,1) = Y(i,1) + e(i,1);
end
for k=2:smpl+1
Y_1(k,1)=Y(k-1,1);
end
dY=Y-Y_1;
rhohat(j,1)=(Y_1(2:smpl+1,1)'*dY(2:smpl+1,1))/(Y_1(2:smpl+1,1)'*Y_1(2:smpl+1,1));
ehat=dY - rhohat(j,1)* Y_1;
tau(j,1) = rhohat(j,1) / sqrt(((ehat'*ehat)/(smpl-1))/ (Y_1'*Y_1));
end
a=smpl*rhohat;
x=[-30:0.1:5];
subplot(3,1,1)
hist(a,x)
subplot(3,1,2)
hist(tau,x)
subplot(3,1,3)
n=max(repl,smpl);
wn=randn(n,1);
hist(wn,x)
CriticalValue=quantile(tau,0.05)
위의 코드는 오래된 버전에서도 동작하도록 만들었습니다. lagmatrix(lagged variable을 만드는 함수), regress(회귀분석 함수)등과 같은 함수가 내장되어 있는 버전의 경우 더 쉽게 할 수 있습니다.
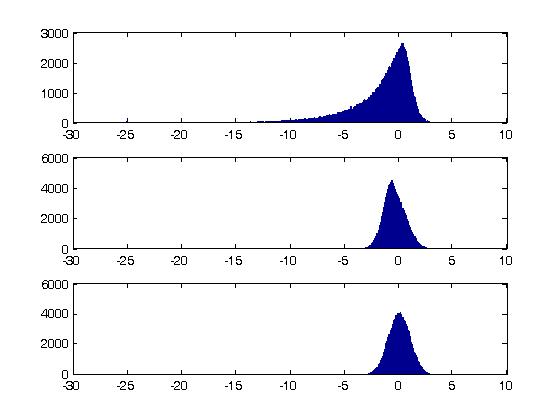
아래는 샘플수를 1000, 반복횟수를 100000번으로한 결과입니다.
첫번째 결과는 unit root Distribution입니다. 왼쪽으로 꼬리가 긴 것을 알 수 있습니다.
두번째 결과는 tau Distribution입니다. 맨 아래의 standard normal과 비교해볼 때 왼쪽으로 최빈값이 치우쳐 있음을 알 수 있습니다. 또한 5% 유의수준의 임계값도 계산해본 결과 -1.9469로, 표준정규분포일 때 5% 유의수준이 -1.645임을 감안하면 왼쪽에 있다는 것을 알 수 있습니다.
Matlab으로 시뮬레이션하였습니다. 파일첨부가 안돼서 m-file을 올리지 못하여 그냥 긁어 붙입니다. 실행해보는 방법은 다음과 같습니다.
1. MATLAB에 File->New->M-file여시고 아래 내용을 긁어다 붙입니다.
2. 저장하실 때 dicful.m으로 저장합니다. (아마 default로 되어있을 겁니다.)
3. command 창에서 dicful(샘플수, 시뮬레이션 반복 수)를 입력하고 엔터.
ex) 1000개의 샘플을 가지고 10000번 시뮬레이션 돌리고 싶으면, dicful(1000,10000) 입력
function f=dicful(smpl, repl)
Y=zeros(smpl+1,1);
Y_1=zeros(smpl+1,1);
rhohat=zeros(repl,1);
tau=zeros(repl,1);
for j=1:repl
randn('state',j)
e=randn(smpl,1);
for i=1:smpl
Y(i+1,1) = Y(i,1) + e(i,1);
end
for k=2:smpl+1
Y_1(k,1)=Y(k-1,1);
end
dY=Y-Y_1;
rhohat(j,1)=(Y_1(2:smpl+1,1)'*dY(2:smpl+1,1))/(Y_1(2:smpl+1,1)'*Y_1(2:smpl+1,1));
ehat=dY - rhohat(j,1)* Y_1;
tau(j,1) = rhohat(j,1) / sqrt(((ehat'*ehat)/(smpl-1))/ (Y_1'*Y_1));
end
a=smpl*rhohat;
x=[-30:0.1:5];
subplot(3,1,1)
hist(a,x)
subplot(3,1,2)
hist(tau,x)
subplot(3,1,3)
n=max(repl,smpl);
wn=randn(n,1);
hist(wn,x)
CriticalValue=quantile(tau,0.05)
위의 코드는 오래된 버전에서도 동작하도록 만들었습니다. lagmatrix(lagged variable을 만드는 함수), regress(회귀분석 함수)등과 같은 함수가 내장되어 있는 버전의 경우 더 쉽게 할 수 있습니다.
아래는 샘플수를 1000, 반복횟수를 100000번으로한 결과입니다.
첫번째 결과는 unit root Distribution입니다. 왼쪽으로 꼬리가 긴 것을 알 수 있습니다.
두번째 결과는 tau Distribution입니다. 맨 아래의 standard normal과 비교해볼 때 왼쪽으로 최빈값이 치우쳐 있음을 알 수 있습니다. 또한 5% 유의수준의 임계값도 계산해본 결과 -1.9469로, 표준정규분포일 때 5% 유의수준이 -1.645임을 감안하면 왼쪽에 있다는 것을 알 수 있습니다.
